
![]()
Boosting, zayıf öğrenicileri(weak learner) güçlü öğreniciye(strong learner) dönüştürme yöntemidir. Bunu iterasyonlar ile aşamalı olarak yapar. Boosting algoritmaları arasındaki fark genellikle zayıf öğrenicilerin eksikliğini nasıl tanımladıklarıdır. Bu yazıda öncelikle Gradient Boosted Regresyon Ağaçları algoritmasının çalışma mantığı ve Python ile adım adım nasıl uygulandığı, sonrasında ise kısaca teorisi anlatılacaktır.
Gradient Boosting’de öncelikli olarak ilk yaprak(initial leaf) oluşturulur. Sonrasında tahmin hataları göz önüne alınarak yeni ağaçlar oluşturulur. Bu durum karar verilen ağaç sayısına ya da modelden daha fazla gelişme kaydedilemeyinceye kadar devam eder.
Konu örnek veri seti üzerinden uygulama ile anlatılacaktır. Bu sebeple aşağıda veri seti tanımlanmış ve kullanıma hazır hale getirilmiştir. Veri setine link‘ten ulaşabilirsiniz.
#gerekli kütüphaneler eklenmiştir.
import os
import pandas as pd
import numpy as np
from warnings import filterwarnings
filterwarnings('ignore')#veri seti tanımlanmıştır.
os.chdir('.../Gradient_Boosting_Regression/california-housing-prices/')
df= pd.read_csv('housing.csv')#konunun kolay açıklanması için veri setinden az sayıda satır ve sutun kullanılacaktır. df=df.sample(n=5, random_state=2) df=df[['housing_median_age','households','median_house_value','median_income']] df.head()

İlk olarak tahminlenecek değişkenin(hedef değişken) ortalaması alınır. Bu sayı ilk tahmin girişimimiz olan ilk yapraktır.
df['initial_leaf']=df["median_income"].mean() df.head()

Bu değer ile hedef değişken karşılaştırılarak ne kadar hatalı tahminleme yapıldığı gözlemlenir. Hata(residual), gözlemlenen değerden tahmin edilen değerin çıkarılması ile bulunmaktadır.
df["residual1"]=df["median_income"]-df["initial_leaf"] df.head()

1. ağaç, ilk yaprak sonucunda elde edilen hataları tahminleyen bir model olarak kurulacaktır.
#kurulacak karar ağacı için bağımlı ve bağımsız değişkenler tanımlanmıştır. X=df[['housing_median_age', 'households', 'median_house_value']] y=df[['residual1']]
#model kurulmuştur. from sklearn.tree import DecisionTreeRegressor regressor = DecisionTreeRegressor(max_depth=3, max_leaf_nodes=4) regressor.fit(X,y)
#veri görselleştirmesi için export_graphviz kütüphanesi kullanılmıştır.
from sklearn.tree import export_graphviz
import matplotlib.pyplot as plt
export_graphviz(regressor, out_file='tree.dot', feature_names=X.columns)
from IPython.display import Image
Image("tree.png")
İlk tahmin ve ilk ağaçtan çıkan sonuçları toplarsak hedef değişkeni %100 doğru tahmin edebiliriz. (Ağaçlarda yapraklardan daha fazla residual olabilir, bazı residuallar aynı yaprağın içine girecektir. Bu olduğunda, ortalamaları hesaplanır ve yaprak içine yerleştirilir. Bu sebeple her zaman %100 doğru tahmin gerçekleşmeyebilir.) Ancak bu durum aşırı öğrenmedir.
df['tree1_result'] = regressor.predict(X) df.head()
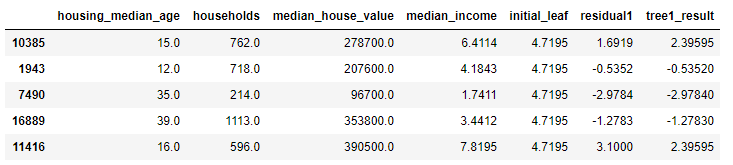
Gradient Boosting bu sorunu aşmak için ağaçlara öğrenme oranı (learning rate) ekler. Bu değer 0 ile 1 arasındadır.
Bu çalışmada learning rate 0,1 olarak tanımlanmıştır. Sonuç olarak tahmin ilk yaprak + learning rate*1.ağaç olarak hesaplanacaktır.
df['tree1_result'] = df['tree1_result']*0.1 df['pred1'] = df['initial_leaf'] + df['tree1_result'] df.head()

Learning rate ile ölçeklendirilmiş tahmine göre hata hesaplandığında sonuç aşağıdaki gibidir.
df['residual2'] = df["median_income"]-df["pred1"] df.head()

residual1 ve residual2 kolonları incelendiğinde doğru tahmine yaklaşıldığı, daha az hata yapıldığı görülmektedir.
Gradient Boosting’i geliştiren istatistikçi Jerome H. Friedman’a göre hedefe ulaşmak için birçok küçük adım kullanmak test datasında daha iyi sonuç vermekte, varyansı düşürmektedir.
3. adım olarak doğru tahmine daha çok yaklaşabilmek adına bir önceki ağacın hataları baz alınarak yeni ağaç kurulur.
X=df[['housing_median_age', 'households', 'median_house_value']]
y=df[['residual2']]
from sklearn.tree import DecisionTreeRegressor
regressor = DecisionTreeRegressor(max_depth=3, max_leaf_nodes=4)
regressor.fit(X,y)
from sklearn.tree import export_graphviz
import matplotlib.pyplot as plt
export_graphviz(regressor, out_file='tree2.dot', feature_names=X.columns)
from IPython.display import Image
Image("tree2.png")
Şimdi ilk yaprak, önceki ağaç ve yeni ağaç kombinlenerek yeni tahmin elde edilecektir.
Hesaplama, ilk yaprak + learning rate*1.ağaç+ learning rate*2.ağaç şeklinde olacaktır.
df['tree2_result'] = regressor.predict(X) df['tree2_result'] = df['tree2_result']*0.1 df['pred2'] = df['initial_leaf'] + df['tree1_result'] + df['tree2_result'] df['residual3'] = df["median_income"]-df["pred2"] df[['median_income','initial_leaf','pred1','pred2','residual1','residual2','residual3']].head()

Doğru sonuca ulaşmak için ufak bir adım daha atılmıştır.
Yeni ağaç üretimi, daha önce belirtildiği gibi, belirlenen ağaç sayısına ya da ağaç eklenmesi anlamlı olmayıncaya kadar devam edecektir.
TEORİ
Gradient Boosted Regresyon Ağaçları 4 adımda hesaplanmaktadır.
1.Adım
Kayıp fonksiyonu(loss function) tanımlanır. Kayıp fonksiyonu, modelin katsayılarının temel alınan veriye uymada ne kadar iyi olduğunu gösteren bir ölçüdür.
Aşağıdaki formül ile gösterilir.

yi gözlemlenen değer, F(x) tahmin edilen değerdir.
Bir çok kayıp fonksiyonu vardır. Gradient Boosted Regresyon Ağaçları’nda yaygın olarak kullanılanı ½(gözlemlenen değer – tahminlenen değer)^2 formülü ile elde edilendir. Yazıda bu kayıp fonksiyonu ile çalışılmıştır.
Gradient Boosting hesaplamasında türev çok fazla kullanılır. Bu formülün tahminlenen değere göre türevi alındığında ½ değeri yok olur ve –(gözlemlenen değer-tahminlenen değer) sonucuna ulaşılır. Bu kolaylık sebebiyle formülün başına ½ getirilmektedir.
2.Adım
Sabit değişken belirlenir.

Formülde sigma’nın içindeki değer kayıp fonksyonudur. yi gözlemlenen değer, Y(gamma) tahminlenen değeridir.
Tüm gözlemler için kayıp fonksiyonu toplanacak ve değerinin minimum hali bulunacaktır. Bunun için kayıp fonksiyonunun türevi alınır, değerler toplanır ve sıfıra eşitlenir. Sonuç olarak initial leaf bulunur. Bu değer hedef değişkendeki tüm değerlerin ortalamasına eşittir.
3.Adım
3. adım 4 aşamada gerçekleşmektedir ve tüm ağaçlarda uygulanacak bir döngüdür.
Önceki tahmine göre hatalar hesaplanır.
Formülde r, residual anlamına gelmektedir. i gözlem numarası, m kurulan ağacın numarasını ifade eder.
Parantez içi türevi alınmış kayıp fonksiyonudur. Parantez dışında bakıldığında F(x) değerinin bir önceki ağacın çıktısını ifade ettiği görülmektedir.
Bu formül ile tüm gözlemler için kalıntılar hesaplanır.
Sonrasında residual’lar için karar ağacı oluşturulur ve her yaprağın değeri bulunur.

Formül her yaprak için hatayı minimize eder. (2. Adımda olduğu gibi, ancak burada formül Fm-1’i yani bir önceki tahmin değerini kullanır.)
Yine aynı şekilde kayıp fonksiyonunun türevi alınır ve değerler toplanıp sınıfa eşitlenir. Çıkan sayı yaprağın değeridir.
Her gözlem için tahmin oluşturulur.
Formül incelendiğinde F(x)=önceki ağacın sonuçları + learning rate*yeni ağaç olduğu görülmektedir.
Döngü bu şekilde devam edecektir.
SONUÇ
Bu yazı Gradient Boosted Regresyon Ağaçları algoritmasının temel olarak nasıl çalıştığı anlatılmaya çalışılmıştır. Algoritmaların arkasında yapı bilindiği zaman hiperparametreler konusunda daha iyi yorum yapılacak ve çeşitli sorunların önüne geçilebilecektir. Umarım faydalı olmuştur. Diğer yazılarıma ulaşmak için link‘e tıklayabilirsiniz.
KAYNAKLAR
Gradient boosting machines, a tutorial – Alexey Natekin, Alois Knoll
https://towardsdatascience.com/understanding-gradient-boosting-machines-9be756fe76ab

