Korelasyon Analizi(r) Nedir?

Ecem Esra Öztürk 27 Haziran 2020 Genel bir bakış, İstatistik 1 116727 1053 kelime - 7 dakika198

Bu yazıya puan ver

(7 votes, average: 3,43 out of 5)

Merhaba. Bu yazımda korelasyon analizi nedir ve nasıl uygulanır sorularını açıklamaya çalıştım. Keyifli okumalar.

Korelasyon analizi; değişkenler arasındaki ilişki, bu ilişkinin yönü ve şiddeti ile ilgili bilgiler sağlayan istatiksel bir yöntemdir.

İki ya da daha çok değişken arasındaki ilişkinin matematiksel bağıntısı “Regresyon Analizi” ile ilişkinin yönü ve derecesi ise “Korelasyon Analizi” ile incelenir.

Korelasyon katsayısı, bağımlı değişken ile bağımsız değişkenler arasındaki ilişkinin gücünü gösteren bir katsayıdır. Örneğin; öğrencinin ders çalışma süresi ile aldığı istatistik notu arasında ilişki olup olmadığını veya borsada işlem gören bir hisse senedinin belli bir dönemdeki günlük getirisi (X) ile içinde yer aldığı bir endeksin günlük getirisi (Y) arasındaki ilişki korelasyon katsayısı ile incelenebilir. Korelasyon katsayısı değişkenlerin yönü ve etkileşimlerin nasıl olduğu hakkında bilgi verir.

Korelasyon katsayısı, açıklanan varyans açıklanamayan varyans oranı olarak tanımlanır.

Korelasyon katsayısı iki değişken arasındaki doğrusal ilişkinin ölçüsü olup incelenen değişkenlerin birimlerinden bağımsızdır ve -1 ≤ r ≤1 arasındadır. Yani 5 ya da -5 olamaz. Korelasyon katsayısının 0’a yaklaşması değişkenler arasında zayıf ilişkinin varlığını gösterir. Değişkenler birlikte artıyor veya azalıyorsa pozitif yönde, değişkenlerden biri artarken diğeri azalıyorsa ise negatif yönde bir ilişki vardır.

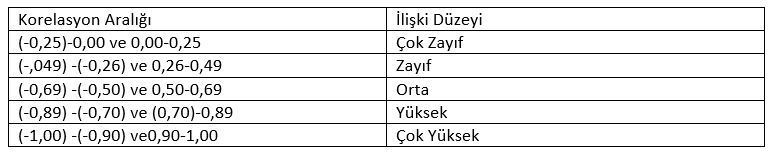
Açıklanan Varyans (Determinasyon Katsayısı) Nedir?

Değişkenlerden birinde gözlenen değişkenliğin ne kadarının diğer değişken tarafından açıklandığını yorumlamada kullanılır ve korelasyon katsayısının karesine eşittir. R²ile gösterilir

r² =1 olması, deneysel verilerin kusursuz doğrusal bir eğri sağlandığını gösterir. r² =0.80 ise, y değişkenindeki toplam varyasyonun %80’i açıklanabilirken %20’si açıklanamaz anlamına gelmektedir.

Korelasyon katsayısı, hipotez testi önemli ve anlamlı bulunduğunda kullanılır. r₁₂; X1 ve X2 bağımlı değişkenleri arasındaki basit korelasyon katsayısı, r örneklem korelasyon katsayısı, p ise ana kütle korelasyon katsayısı olmak üzere;

r= XYOAÇT/ √(XOAKT)*(YOAKT) olarak verilir. Bunlar bir değere ait x (bağımsız) ve y (bağımlı) değişkenleri arasındaki ilişkiyi, ilişkinin yönü ve şiddetini belirlememizi sağlayan formüllerdir. X’in, y’nin ve xy çarpımının ortalamaya uzaklığının kareler toplamı olarak hesaplanırlar.

X Ortalamadan Ayrılış Kareler Toplamı (XOAKT)

XOAKT=∑X²-(∑X)²/n Yani toplam x’in karesinin n’e bölümünden çıkan sonuç, x’lerin kareleri toplamından çıkarılır.

Y Ortalamadan Ayrılış Kareler Toplamı (YOAKT)

YOAKT=∑y²-(∑y)²/n formülüyle hesaplanır. Yani toplam y’nin karesinin n’e bölümünden çıkan sonuç, y’lerin kareleri toplamından çıkarılır.

XY Ortalamadan Ayrılış Kareler Toplamı (XYOAÇT)

XYOAÇT=∑xy-(∑y*∑x)/n formülüyle bulunur. Yani toplam x ile toplam y çarpılıp n (veri sayısına) bölünür. Elde ettiğimiz sayı, x ve y’lerin çarpımlarının toplamından çıkarılır. Bu şekilde XY ortalamadan ayrılış kareler toplamını elde ederiz.

Ya da X1 ve X2 değişkenlerini x veya y cinsinden yazar ve sadeleştirirsek;

r=n*∑xy-√(∑x)*(∑y)/n*(∑x)*√n*(∑y)-(∑y)

ÖRNEK: Bir fabrika bünyesindeki satış personeli sayısı ile satış gelirleri arasındaki ilişki bilinmek istenmektedir. Korelasyon katsayısını ve korelasyon katsayısının önemliliğini hesaplayınız.

Tablo-2: Satış Personeli ve Satış Gelirleri

Çözüm:

Basit (İkili) Korelasyon, bir değere ait iki ölçüm olduğunda bu iki değişken arasındaki ilişkiyi belirler. Bu değişkenlerden birinin sabitlenerek diğer değişkenler ile olan ilişkisi ise kısmi korelasyon teknikleriyle hesaplanır.

Kısmi Korelasyon terimi ilk kez 1907 yılında Yule tarafından kullanılmıştır.

X değişkeni, bağımız değişkendir. Yani başka bir değişkene bağlı olmadan artıp azalır. Y değişkeni ise bağımlı değişkendir.

Bu soruya göre; satış gelirleri (y), satış personeli (x) sayısına bağlı olarak artıp azalmaktadır.

n=10,

Σx=281

Σy=26

(Σx)²=78961

(Σy)²=676

Σ(xy)=791.67

Σx²=8859

Σy²=74.4012

r= XYOAÇT/ √(XOAKT)*(YOAKT) formülünden

r=61,07/√(962*68012)=0,00755

İstatiksel karar: Üretimde çalışan personel sayısı ile üretim miktarının arasında pozitif ve güçlü bir ilişki vardır.

Korelasyon Katsayısının Anlamlılık Düzeyi

Örnek değerlerin korelasyon katsayısı(r) ile ana kütlenin teorik korelasyon katsayısı olan rho’nun (p) tahmin edilmesidir.

Hipotez;

H0: p=0

Hs: p>0

şeklinde kurulur. Korelasyon katsayısının anlamlılığı t testi kullanılarak, n-2 serbestlik derecesine göre aşağıdaki işlemler dahilinde verilen anlamlılık düzeyine göre test edilir. Test istatistiği;

t_H=r/√(1-r²/n-2) ile hesaplanır.

Verilen anlamlılık düzeyi (α) için; t_H>t_α:n-2 olduğunda H₀ reddedilecek ve Hs ise kabul edilecektir. Yani; r korelasyon katsayısının istatiksel olarak anlamlı ve değişkenler arasında bir ilişki olup olmadığı görülecektir.

Yukarıda bulduğumuz korelasyon katsayısını 0,05 anlamlılık düzeyinde test edelim.

Çözüm:

H0: p=0 (Korelasyon katsayısı önemsizdir.)

Hs: p ≠ 0 (Korelasyon katsayısı önemlidir.)

t_h=r/S_r=r/√(1-r²/n-2)=0,00755/√(1-0,00755²/(10-2))=0,999

t_T=t _α/2;n-2=t_0,025;8=2,306 olarak bulunur.

|t_h|<t_T olduğundan H0 reddedilir.

İstatistiksel karar: Korelasyon katsayısı anlamlı ve önemlidir.

Başka bir yazıda görüşmek dileğiyle hoşça kalın.

Kaynaklar