![]()
Merhaba arkadaşlar, Zaman Serileri Çözümlemesi yazı serisinin yanında ara ara bir kaç küçük çözümlemelerde yapacağım. Bu çözümlemelere çerez diye tabir etmek istiyorum. Şu anki çerezimiz 2×2’lik tabloların R ile çözümlenmesidir. Çözümlemeye geçmeden önce Ki Kare dağılımıyla ilgili bilgiler verelim.
Ki kare, örnekleme yoluyla elde edilen verilerin, kitle gözlemlerine uygun olup olmadığını başka bir deyişle gözlenen sıklıkların(frekansların), beklenen sıklıklara uygun olup olmadığı ki kare testiyle tespit edilir.
Normal dağılımın Zi değerlerin karesi alındığında, Zi2 değerlerinin dağılımı Ki Kare(χ2) dağılımına dönüşür.
Bu teorik bilgiyi verdikten sonra asıl bizi ilgilendiren kısma geçelim. 2×2’lik tablolarda ki kare çözümlemesi nasıl yapılır?
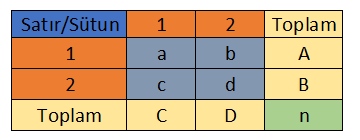
Yandaki tabloda görüldüğü üzere 2×2’lik tabloların gösteriş biçimi bu şekildedir.
- A =Birinci satırın toplamı
- B =İkinci satırın toplamı
- C =Birinci sütunun toplamı
- D =İkinci sütunun toplamı
- n = Toplam örneklem genişliği olmak üzere.
Eğer tablodaki gözlemlerde a,b,c,d değerlerinden en az biri 5’ten küçük ise Fisher’ın Kesin Ki Kare Testi yapılır. Örnek tablo göstermek gerekirse;

Yukarıdaki verileri Fisher’ın Kesin Ki KareTesti ile yaparız. Çünkü kanser olan ve sigara içmeyenlerin örneklem genişliği 4’tür ve bu değer 5’ten küçüktür.
Fisher’ın Kesin Ki Kare Testi Formülü:
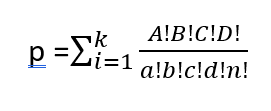
Şimdi R’da bu öğrettiklerimizi uygulayalım.
Çözümleme 1
Verilerimizin içeriği, sigara içme durumu ile kanser olma arasındaki bağlantıyı çözmemize yönelik verilerdir.
veri <- matrix(c(4,82,75,15), nrow=2, dimnames=list(c("sigara içmiyor", "sigara içiyor"), c("kanser var", "kanser yok")))
veri # 5 den küçük gözlem olduğu için Fisher'ın ki karesini yapmamız lazımÇıktı:

Evet verileri girip tabloyu çıkarttığımızda 5’ten küçük gözlem olduğunu görüyoruz. O zaman Fisher’ın Kesin Ki Kare Testini yapmamız lazım.
Testi yapmadan önce hipotezimizi kurmamız lazım.
H0: Sigara içme durumu ile kanser olma arasında bir ilişki yoktur.
H1: Sigara içme durumu ile kanser olma arasında bir ilişki vardır.
Hipotezi kurduğumuza göre şimdi test edebiliriz.
fisher.test(veri)
Çıktı:
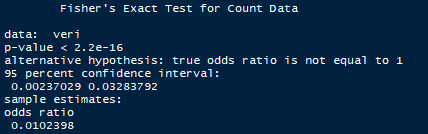
p değerine baktığımızda α = 0.05 değerinden çok küçük olduğunu bu sebepten dolayı yokluk hipotezimizin(H0) reddedileceğini %5 anlamlılık düzeyinde istatistiksel olarak söyleyebiliriz. O zaman sigara içme durumu ile kanser olma arasında bir ilişki var bunu hipotezden söyleyebiliyoruz. Peki bu ilişkinin miktarı nedir ve bu ilişki miktarı anlamlı mıdır?
Verilerimiz sınıflanabilir(nominal) olduğu için Cramer’s V ile bu ilişki miktarı ölçülebilir. İlişkinin anlamlılık hipotezini kuralım.
H0: Sigara içme durumu ile kanser olma arasındaki ilişki anlamsızdır.(Φ = 0)
H1: Sigara içme durumu ile kanser olma arasındaki ilişki anlamlıdır.(Φ ≠ 0)
library(DescTools) CramerV(veri, conf.level = 0.95) # 0.79luk ilişki ve anlamlı
Çıktı:
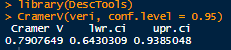
Yukarıdaki R çıktısında bu ilişkinin anlamlılığını ölçmek için bir güven aralığı verildiğini görüyoruz. Güven aralığı yokluk hipotezindeki 0 değerini içermediği için yokluk hipotezimizin yani sigara içme durumu ile kanser olma arasındaki ilişki anlamsızdır hipoteziniz reddedildiği görülmektedir. Öyleyse toparlayacak olursak. Sigara ile kanser arasındaki ilişkinin %79 ve anlamlı olduğu %5 güven düzeyinde istatistiksel olarak söylenebilir.
Genel Yorum: Sigara ile kanser arasında bir ilişki olduğu ve bu ilişkinin anlamlı ve %79’luk güçlü sayılabilecek bir ilişkiye sahip olduğunu %5 güven düzeyinde istatistiksel olarak söyleyebiliriz.

Eğer yandaki tablo değerlerinin hepsi 5’ten büyükse ve beklenen sıklıkları 25’den küçükse Süreklilik Düzeltmeli(Yates) Ki Kare testi, eğer beklenen sıklıkları 25’den büyükse Pearson ki kare testi uygulanabilir.
Beklenen sıklık hesaplama:
- 1.satır 1. sütun için : (A*C)/n
- 1.satır 2. sütun için: (A*D)/n
- 2.satır 1. sütun için: (C*B)/n
- 2.satır 2. sütun için: (D*B)/n
Yukarıdaki yazılanları formülize etmek gerekirse:
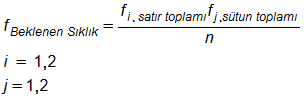
Pearson Ki Kare Formülü:
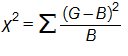
Süreklilik Düzeltmeli(Yates) Ki Kare Formülü:
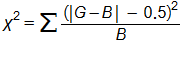
- G = Gözlenen Değer
- B = Beklenen Sıklık
Bu bilgileri de verdikten sonra R’da uygulamaya geçebiliriz.
Çözümleme 2
H0: Ailede kanser olma durumu ile kişinin kanser olması arasında bir ilişki yoktur.
H1: Ailede kanser olma durumu ile kişinin kanser olması arasında bir ilişki vardır.
veri2 <- matrix(c(34,13,19,34), nrow = 2, dimnames=list(c("ailede yok", "ailede var"), c("kanser yok", "kanser var")))
veri2Çıktı:
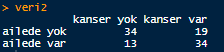
Yukarıdaki tabloda değerlerin 5’den büyük olduğu görülüyor ama beklenen sıklıkları neler?
satir1 <- 34+19
satir1
satir2 <- 13+34
satir2
sutun1 <- 34+13
sutun1
sutun2 <- 19+24
sutun2
n <- sutun1+sutun2
bek_sikliklar <- matrix(c((sutun1*satir1)/n,(sutun1*satir2)/n,(sutun2*satir1)/n,(sutun2*satir2)/n),
nrow = 2)
bek_sikliklarÇıktı:
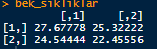
Yukarıdaki çıktıya baktığımızda beklenen sıklıkların 2 tanesinin 25’ten küçük olduğu görülüyor. Öyleyse Süreklilik Düzeltmeli(Yates) Ki Kare yapmamız gerekmektedir.
chisq.test(veri2, correct = T) #ilişki var
Yukarıdaki R kodunda correct parametresine T yazınca Süreklilik Düzeltmeli Ki Kare yapıyor.
Çıktı:

Yukarıdaki çıktıyı p değeri veya Ki Kare tablosu varsa Ki Kare tablosuyla test edebiliriz ama p değeriyle test etmek her zaman daha kolaydır. p = 0.0005 bu değer α = 0.05 değeriden küçük olduğu için yokluk hipotezi reddedilir. Öyleyse ailede kanser olma durumu ile kişinin kanser olması arasında bir ilişki olduğu %5 anlamlılık düzeyinde istatistiksel olarak söylenebilir. Peki ilişki miktarı nedir ve anlamlı mıdır?
Verilerimiz sınıflanabilir(nominal) olduğu için Cramer’s V ile bu ilişki miktarı ölçülebilir. İlişkinin anlamlılık hipotezini kuralım.
H0: Ailede kanser olma durumu ile kişinin kanser olması arasındaki ilişki anlamsızdır.(Φ = 0)
H1: Ailede kanser olma durumu ile kişinin kanser olması arasındaki ilişki anlamlıdır.(Φ ≠ 0)
CramerV(veri2, conf.level = 0.95) #ilişki anlamlı
Çıktı:
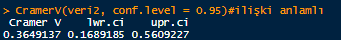
Yukarıdaki R çıktısında bu ilişkinin anlamlılığını ölçmek için bir güven aralığı verildiğini görüyoruz. Güven aralığı yokluk hipotezindeki 0 değerini içermediği için yokluk hipotezimizin yani ailede kanser olma durumu ile kişinin kanser olması arasındaki ilişki anlamsızdır hipoteziniz reddedildiği görülmektedir. Öyleyse toparlayacak olursak. Ailede kanser olma durumu ile kişinin kanser olması arasındaki ilişki %36 ve anlamlı olduğu %5 güven düzeyinde istatistiksel olarak söylenebilir.
Genel Yorum: Ailede kanser olma durumu ile kişinin kanser olması arasındaki %36’lık zayıf sayılabilir bir ilişki olduğu ve bu ilişkinin anlamlı olduğu %5 anlamlılık düzeyinde istatistiksel olarak söylenebilir.
Çözümleme 3
Çözümleme 2 ile aynı konuda olan başşka bir araştırma verileri ile çalışalım.
H0: Ailede kanser olma durumu ile kişinin kanser olması arasında bir ilişki yoktur.
H1: Ailede kanser olma durumu ile kişinin kanser olması arasında bir ilişki vardır.
veri3 <- matrix(c(41,26,72,60), nrow = 2, dimnames=list(c("ailede yok", "ailede var"), c("kanser yok", "kanser var")))
veri3Çıktı:

Yukarıdaki tabloda değerlerin 5’den büyük olduğu görülüyor ama beklenen sıklıkları neler?
satir1_1 <- 41+72
satir2_1 <- 26+60
sutun1_1 <- 41+26
sutun2_1 <- 72+60
n1 <- sutun1_1+sutun2_1
bek_sikliklar_1 <- matrix(c((sutun1_1*satir1_1)/n1,
(sutun1_1*satir2_1)/n1,
(sutun2_1*satir1_1)/n1,
(sutun2_1*satir2_1)/n1), nrow = 2
)
bek_sikliklar_1Çıktı:
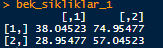
Yukarıdaki çıktıya baktığımızda beklenen sıklıkların hepsinin 25’ten büyük olduğu görülüyor. Öyleyse Pearson Ki Kare yapmamız lazım.
chisq.test(veri3, correct = F)
Çıktı:

Yukarıdaki çıktıyı p değeri veya Ki Kare tablosu varsa Ki Kare tablosuyla test edebiliriz ama p değeriyle test etmek her zaman daha kolaydır. p = 0.3709 bu değer α = 0.05 değeriden büyük olduğu için yokluk hipotezi reddedilemez.Yani ilede kanser olma durumu ile kişinin kanser olması arasında bir ilişki olmadığı %5 anlamlılık düzeyinde istatistiksel olarak söylenebilir. Eğer ilişki yoksa miktarını ölçmek anlamsız olacağı için bu çözümleme burada bitmiş olur.
Bu yazımız burada bitmiştır. Diğer yazılarımızda görüşmek üzere kendinize iyi bakın iyi günler dilerim 🙂