![]()
Python ile çoklu lineer regresyon yazımıza devam ediyoruz. Geçen yazıda veri setini eğitim ve test olmak üzere ayırmıştık. Bu yazımızda makinemizi oluşturup eğiteceğiz. Yine scikit-learn linear_model kütüphanesinden LinearRegression sınıfını kullanacağız.
Çoklu Lineer Modeli Eğitmek
from sklearn.linear_model import LinearRegression regressor = LinearRegression() regressor.fit(X_train, y_train)
Makinemizi (regressor) eğittik. Şimdi test edelim bakalım bize ne sonuçlar veriyor. Bunun için LinearRegression sınıfından oluşturduğumuz regressor nesnesinin (yani makinemizin) fit() metodunu kullanacağız. Bu metoda parametre olarak da test için ayırdığımız 10 elemanlı X_test nitelikler matrisini vereceğiz.
y_pred = regressor.predict(X_test)
Eğitilmiş Modelde Test Verilerini Çalıştırmak ve Sonuçları Kıyaslamak
Evet, test verisinden oluşan tahmin verilerimiz (y_pred) ile y_test‘i tablo halinde yan yana görelim. Bakalım makinemiz bize hangi sonuçları üretmiş ve bunların gerçek sonuçlardan farkı nasıl?
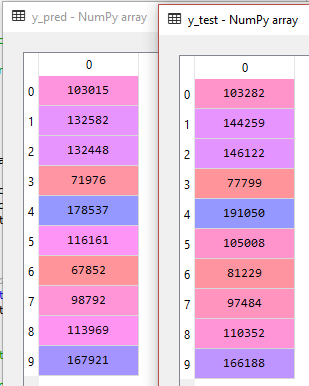
Solda tahmin ettiğimiz 10 değere karşılık sağ tarafta gerçekte var olan 10 değer. 0’ıncı indeksteki kar sonuçlarını karşılaştıralım. Eğittiğimiz model bize test setindeki bağımsız değişkenleri verdiğimizde sonucun 103.015 TL olacağını söylüyor. Buna karşılık aynı bağımsız değişkenler ile gerçek kar 103.282 TL olarak gerçekleşmiş. Çok iyi bir tahmin. Diğer satırları siz karşılaştırın ve modelin nasıl bir iş çıkardığı hakkında kabaca bir yorum yapın.
Geriye Doğru Eleme Yöntemi ile Modeli Kurmak
İki önceki yazımızda regresyon modeli kurma yöntemlerinden bahsetmiştik. Burada bu yöntemlerden geriye doğru eleme ile modelimizi optimize edeceğiz. Aşağıda standart bir çoklu doğrusal regresyon eşitliği görülmektedir.
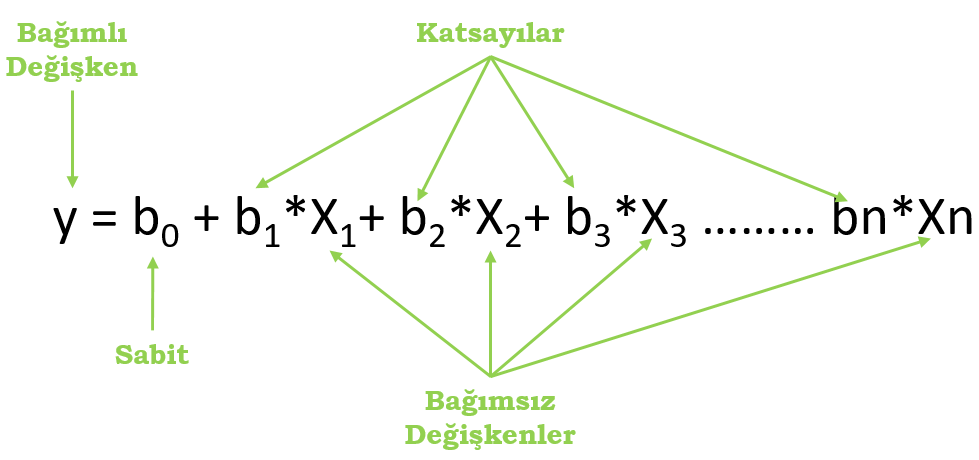
Yukarıda gördüğümüz eşitlikte bağımsız değişkenler (X1,X2…Xn) X nitelikler matrisinde bulunan her bir niteliğe (sütun) karşılık gelmektedir. Biz bu bağımsız değişkenleri kullanarak modeli eğitir ve b1,b2,,,bn’den olşan katsayıları hesaplamaya çalışırız. Pekala yukarıdaki eşitlikte bir şey dikkatinizi çekti mi? Niçin katsayılar b0‘dan başlayıp bn‘e kadar giderken bağımsız değişkenler X1‘den başlıyor? X0 yok mudur? Aslında var. b0‘ın başında 1 var diyelim. Biliyoruz ki 1’ile b0‘ı çarpmak sonucu değiştirmez. Yani böylece b0 önünde X0 olmuş ve o da 1’e eşit olmuş olur.
X = np.append(arr = np.ones((50,1)).astype(int), values = X, axis = 1)
Yukarıdaki kodlarla X nitelikler matrisimizin 0’ıncı indeksine 50 elemanlı 1 sütunlu ve her bir satırında 1 olan bir array ekliyoruz. NumPy kütüphenesinin append() metodunu kullanıyoruz.
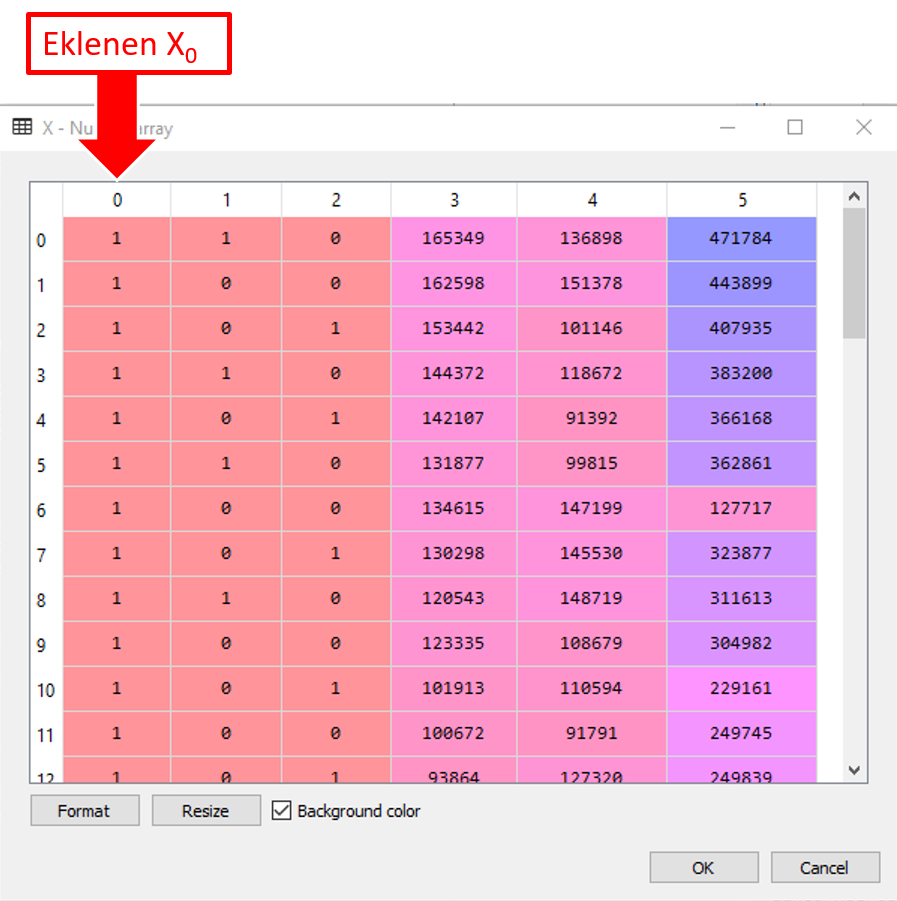
Şimdi geriye doğru eleme yöntemini kullanarak optimal modelimizi seçmeye başlayalım.
İlk adımımız anlamlılık düzeyini seçmekti. 0,05 olarak seçelim (Bunu şimdi bir yere yazmıyoruz. Sadece böyle kabul ettik. Değişken elerken bu kabule göre eleyeceğiz).
İkinci adımımız ise tüm değişkenleri dahil edeceğimiz bir model kurmak: Bunun için öncelikle X nitelikler matrisimizden yeni bir X_opt nitelikler matrisi oluşturalım. Arkasından da yeni makinemizi (regressor_OLS) yaratalım. Bunun için istatistiksel modeller kütüphanesinin OLS (Ordinary Least Squares) sınıfını kullanıyoruz. Bu sınıfın fit() metoduyla makinemizi eğitelim. İşin Türkçesi çoklu regresyonda Sıradan En Küçük Kareler (Ordinary Least Squares) yöntemini kullanmış oluyoruz. Neydi bu yöntem hemen hatırlayalım: Bütün noktaların regresyon doğrusuna uzaklığının karelerinin toplamını en küçük yapan yöntemdi. Böylelikle doğrumuz nitelikler matrisindeki tüm noktaları en iyi şekilde temsil edebiliyordu. Eşitlikçi, adil yaklaşım, adil düzen 🙂 Aklıma basit bir örnek geldi: Uzunlamasına bir ova düşünün ve içinde bir çok tarla olsun. Bu ovadan büyük bir sulama kanalı geçireceksiniz. Bu kanal geçtikten sonra çiftçiler kanala tarlalarından boru uzatacak ve tarlalarının kenarına koydukları su motorlarıyla ürünlerini sulayacaklar. Şimdi kanalı öyle bir yerden geçirelim ki çiftçiler tarafından döşenecek su borularının uzunluğu en az olsun. Hadi çiftçiler kendileri döşemesin boruları üretici kooperatifi kurmuş olsunlar ve kooperatif kanal ve boru döşeme işini ihale etmiş olsun. Şimdi ihaleyi alan şirket kanalı öyle bir hattan (hadi “S” çizmek de yasak olsun, kanal ve borular düz döşenmek zorunda olsun) geçirecek ki her bir çiftçinin tarlasına çekeceği boruların toplam uzunluğu en az olacak, dolayısıyla bu işi en düşük maliyetle yapmış olacak. İşte OLS’nin yaptığı iş aynen budur.
Üçüncü adım için şunları söylemiştik: “Her bir bağımsız değişkenin anlamlılık düzeyi incelenir. Eğer anlamlılık düzeyi model için belirlenenden (ilk adımda 0,05 belirlemiştik) daha büyük ise bu bağımsız değişken modelden çıkarılır. Eğer birden fazla var ise bu işlem en büyük p değerine sahip olana uygulanarak devam edilir. Şayet bütün p değerleri sınır değerden küçük ise model tamam demektir.”
Birinci tur (tüm değişkenlerin dahil olduğu ilk model)
import statsmodels.formula.api as sm X_opt = X[:, [0,1,2,3,4,5]] regressor_OLS = sm.OLS(endog=y, exog=X_opt).fit()
Öyleyse modelimizi çalıştırdık. Şimdi özetini alıp inceleyelim ve üçüncü adımın gereğini yapalım. Eleme işlemine geçmeden önce değişkenlerimizi bir eşleştirelim. Çünkü her elemede model X değişkenlerine küçükten büyüğe numara veriyor. Yanlış değişkeni çıkarmamak için bu eşleştirmeyi yapmanızı öneririm.
| İndeks | Değişken | Bağımsız değişken |
|---|---|---|
| 0 | Sabit | X0 |
| 1 | Istanbul | X1 |
| 2 | Kocaeli | X2 |
| 3 | ArgeHarcamasi | X3 |
| 4 | YonetimGiderleri | X4 |
| 5 | PazarlamaHarcamasi | X5 |
regressor_OLS.summary()

summary() metodu yukarıdaki özeti veriyor. Bu özeti okuyup anlamak ilk bakışta biraz zor gelebilir. Ne bu yahu! bir sürü anlamsız rakam ve ifade. Ne bunlar? diyebilirsiniz. Aslında biraz öğrenince o kadar da zor bir şey olmadığını anlayacaksınız. Hatta ilerleyen zamanda bu özetleri okuyup eleme işlemlerini yapmaktan zevk almaya başlıyorsunuz. Devam edelim. Çıkarma kuralımız en yüksek p değerine sahip değişkeni modelden çıkarmak idi. Kırmızı çerçeveye aldığımız p değerleri sütununda X1‘nin en yüksek p değerine (0.990) sahip olduğunu görüyoruz, öyleyse X1‘yi çıkarıyoruz. X1 nitelikler matrisinde 2’nci indekse denk geliyorsu öyleyse X_opt değişkenimizi 1’nci indeksli sütunu devre dışı bırakarak tekrar oluşturalım ve modeli tekrar çalıştırıp özetini alalım.
İkinci tur
Yeni eşleşme şu şekilde olmalı:
| İndeks | Değişken | Bağımsız değişken |
|---|---|---|
| 0 | Sabit | X0 |
| 2 | Kocaeli | X2 |
| 3 | ArgeHarcamasi | X3 |
| 4 | YonetimGiderleri | X4 |
| 5 | PazarlamaHarcamasi | X5 |
X_opt = X[:, [0,2,3,4,5]] regressor_OLS = sm.OLS(endog=y, exog=X_opt).fit() regressor_OLS.summary()

p değerlerini tekrar incelediğimizde X1‘in (orijinal X matrisinde 2’nci indekse karşılık geldiğini sakın atlamayın) en yüksek p değerine (0.940) sahip oluğunu görüyoruz. Bunu da çıkarıp tekrar devam edelim.
Üçüncü tur
Yeni eşleşme:
| İndeks | Değişken | Bağımsız değişken |
|---|---|---|
| 0 | Sabit | X0 |
| 3 | ArgeHarcamasi | X3 |
| 4 | YonetimGiderleri | X4 |
| 5 | PazarlamaHarcamasi | X5 |
X_opt = X[:, [0,3,4,5]] regressor_OLS = sm.OLS(endog=y, exog=X_opt).fit() regressor_OLS.summary()
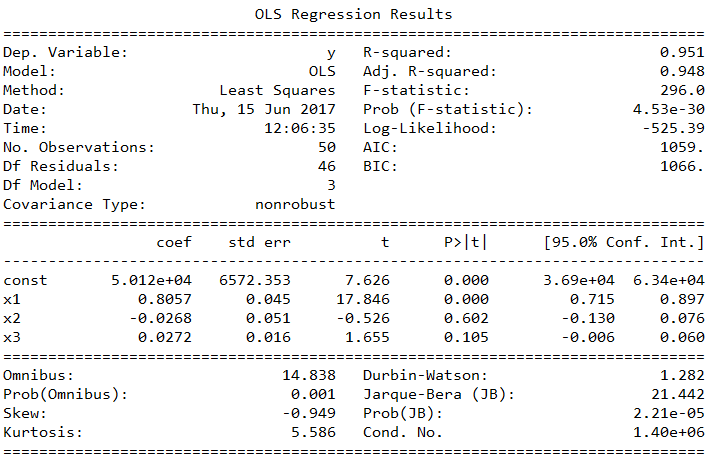
p değerlerini tekrar incelediğimizde X2‘in (orijinal X matrisinde 4’üncü indekse karşılık geldiğini sakın atlamayın) en yüksek p değerine (0.602) sahip oluğunu görüyoruz. Bunu da çıkarıp tekrar devam edelim.
Dördüncü tur
Yeni eşleşme:
| İndeks | Değişken | Bağımsız değişken |
|---|---|---|
| 0 | Sabit | X0 |
| 3 | ArgeHarcamasi | X3 |
| 5 | PazarlamaHarcamasi | X5 |
X_opt = X[:, [0,3,5]] regressor_OLS = sm.OLS(endog=y, exog=X_opt).fit() regressor_OLS.summary()

p değerlerini tekrar incelediğimizde X2‘in (orijinal X matrisinde 5’inci indekse karşılık geldiğini sakın atlamayın) en yüksek p değerine (0.060) sahip oluğunu görüyoruz. Aslında bu değer belirlediğimiz 0.05 anlamlılık değerine çok yakın, çıkarmasak da olur gibi. Neyse burada mevzu bu değil, bunu başka bir zaman tartışalım ve kuralı işletelim.
Beşinci tur
Yeni eşleşme:
| İndeks | Değişken | Bağımsız değişken |
|---|---|---|
| 0 | Sabit | X0 |
| 3 | ArgeHarcamasi | X3 |
X_opt = X[:, [0,3]] regressor_OLS = sm.OLS(endog=y, exog=X_opt).fit() regressor_OLS.summary()
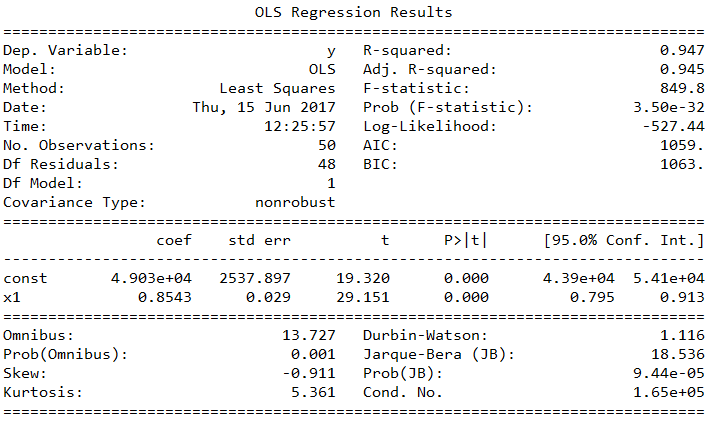
Evet, en sonunda p değerlerini 0.05’in altında bırakmayı başardık. Geriye sabit ve Arge Harcaması kaldı. Yazıyı daha fazla uzatmayalım. Veriyle kalın…
4 Responses
Bir yanıt yazın Yanıtı iptal et
Yorum yapabilmek için oturum açmalısınız.
Güzel makale teşekkürler. Özellikle Tarladaki boruların dağıtımı, en küçük kareler yöntemi için hoş örnek olmuş.
Rica ederim. İyi çalışmalar…
5. Tur görseli 4. tUr ile aynı sanırım. Ellerinize sağlık.
İkazınız için çok teşekkür ederim. Gerekli düzelltmeleri yaptık.