Polinom Regresyon: Python ile Uygulama-1

Erkan ŞİRİN 17 Haziran 2017 Makine Öğrenmesi 5 4468 772 kelime - 5 dakika85

---

Bu yazıya puan ver

(1 votes, average: 5,00 out of 5)

Loading...

---

Basit ve çoklu lineer regresyonda bağımlı değişken ile bağımsız değişkenler arasındaki ilişki doğrusaldı. Ancak gerçek hayatta bazı durumlarda değişkenler arası ilişki doğrusal olmayabilir. Böyle durumlarda ilişkiyi modellemek için Polinom Regresyon kullanılabilir.

Basit lineer regresyon eşitliği: y = c + bX
Çoklu lineer regresyon eşitliği: y = c + b₁X₁ + b₂X₂ …… + b_iX_i
Polinom regresyon: c + b₁X₁ + b₂X²₂ …… b_iXⁱ_i

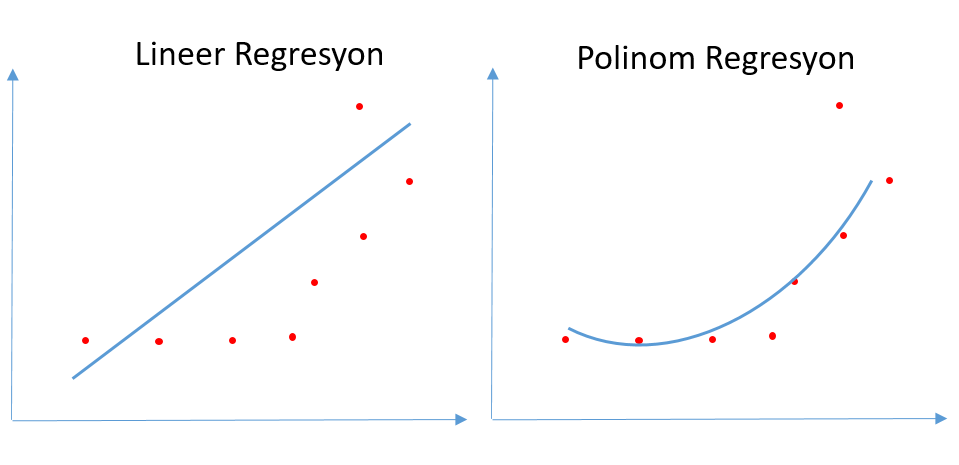
Yukarıdaki basit örnekte verilerin en iyi temsil edecek şekilde geçen doğrunun polinom regresyon doğrusuna ait olduğunu görebiliyoruz. Dolayısıyla her problemi lineer regresyon ile çözemeyiz.

Kütüphaneleri İndirme, Çalışma Diznini Ayarlama ve Veri Setini İndirme

Veriyi buradan indirebilirsiniz.

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import os
os.chdir('Sizin_Calisma_Dizniniz')
dataset = pd.read_csv('PozisyonSeviyeMaas.csv')

Veriyi Anlamak

Yukarıdaki tabloda niteliklerimizi görüyoruz:

Pozisyon: İş Ünvanı. Nitelik türü kategorik.

Seviye:  İş ünvanlarını birbiri arasında maaş, astlık-üstlük vb. sıralayan  nitelik. Nitelik türü nümerik.

Maas: Her bir pozisyondaki personelin yıllık maaşı. Nitelik türü nümerik.

Bu veri seti ve kuracağımız polinom model ile çözmeye çalışacağımız problem seviyesine göre bir personelin maaşını tahmin etmek olacak. Böylelikle y hedef değişkenimizin Maas, bağımsız değişken Seviye olduğunu çıkarabiliyoruz. Pozisyon seviye ile yakından ilgili bir nitelik ve seviyenin adlandırması gibi bir fonksiyonu olduğu için bu niteliği veri setinden çıkarıyoruz.

Veri seti çok az bir kayıttan (10 adet) oluştuğu için eğitim ve test olarak ayırmıyoruz.

Bağımlı ve Bağımsız Değişkenleri Oluşturmak

X = dataset.iloc[:, 1:2].values
y = dataset.iloc[:, 2].values

Değişkenlerin ayrılmış halini yukarıdaki resimde görüyoruz.

Basit Lineer Regresyon ile Modeli Eğitmek

Modelimizi eğitmek için basit ve çoklu doğrusal regresyonda olduğu gibi scikit-learn kütüphanesinden LinearRegression sınıfını kullanacağız. Öncelikle bu sınıftan lin_reg adında bir nesne yaratıyoruz. Daha sonra bu nesnenin fit() metoduna X, y değişkenlerimizi parametre olarak veriyoruz. Böylelikle makinemizi kurmuş oluyoruz (aklıma birden kurmalı saat ve oyuncaklar geldi:) ) Diyeceksiniz ki konumuz polinom regresyon niye basit regresyon yapıyoruz? Karşılaştırabilmek için. Birazdan polinom regresyon da yapacağız.

from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X, y)

Polinom Regresyon için Ön Hazırlık

Polinom regresyon modeli kurmak için öncelikle veri ön işleme yapmamız gerekiyor.

from sklearn.preprocessing import PolynomialFeatures
poly_reg = PolynomialFeatures(degree = 2)
X_poly = poly_reg.fit_transform(X)

Şimdi yukarıdaki kodlar ile neler yaptık? İlk satırda scikit-learn preprocessing modülünden PolynomialFeatures sınıfını indirdik. İkinci satırda bu sınıftan poly_reg adında bir nesne oluşturduk. Nesne oluşurken sınıf ana yapıcısına degree parametresini 2 olarak gönderdik. Bu değer polinomun derecesini belirliyor. Bu nesnenin işi orijinal tek sütunlu X nitelikler matrisini alıp nesnenin fit_transform() metoduyla yeniden biçimlendirmek. Biçimlendirilmiş yeni nitelikler matrisini X_poly adlı değişkene atıyoruz. Yeni nitelikler matrisine göz atalım:

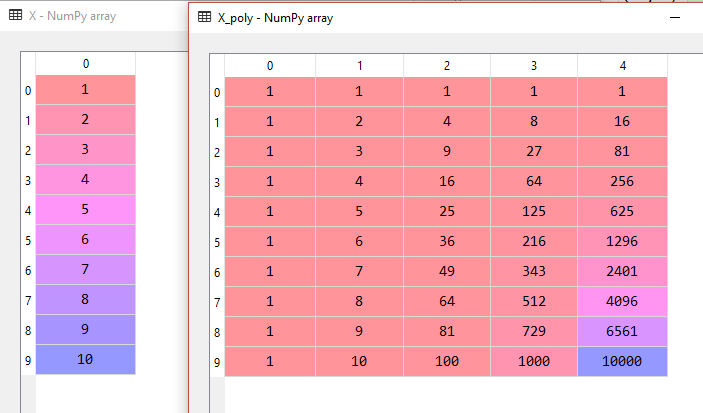
Solda orijinal X nitelikler matrisini, sağda ise X matrisinden türetilmiş yeni polinom nitelikler matrisini görüyoruz. Sağ tarafta X_poly diye adlandırdığımız yeni matrisin 1’inci indeksi orijinal X matrsine karşılık geliyor. İndeks 2 2’nci derece, 3 3’üncü derece, 4 ise 4’üncü derece bağımsız değişkene işaret ediyor. İndeks 0’a dikkat ettiyseniz hepsi 1’lerden oluşmuş. Bu birlerin olduğu nitelik regresyon eşitliğimizdeki sabit katsayının değeri 1’e eşit olan gizli X₀‘a işaret ediyor. Biz başka bir yazımızda bunu elle yapmıştık ancak burada poly_reg nesnesi oluşurken X₀ ile ilgili sütun otomatik olarak yeni matrise eklendi.

Polinom Lineer Regresyon ile Modeli Eğitmek

 Veri ön hazırlığı kapsamında yeni (X_poly) nitelikler matrisini oluşturduk. Şimdi modeli eğitme zamanı:

poly_reg.fit(X_poly, y)
lin_reg_2 = LinearRegression()
lin_reg_2.fit(X_poly, y)

Basit lineer modeldeki LinearRegression sınıfını kullandığımız için nesneler karışmasın diye ikinci lineer model nesnesi için lin_reg_2 nesnesini kullandık. Bu yazıyı burada kesiyorum devamı ikinci yazıda. Veriyle kalın…