Python İle Tek Yönlü Varyans Çözümlemesi(One Way ANOVA)

Osman IŞIK 30 Eylül 2019 Genel bir bakış 0 3513 1254 kelime - 8 dakika91

---

Bu yazıya puan ver

(No Ratings Yet)

Loading...

---

Merhaba VBO severler, bugün Python ile Tek Yönlü Varyans Çözümlemesi yapacağız. Önceki yazılarımdan birinde R ile Tek Yönlü Varyans Çözümlemesine yer vermiştim o yazıya da buradan ulaşabilirsiniz. Varyans Çözümlemesi iki ya da daha fazla grubun ortalamaları arasında istatistiksel olarak bir fark olup olmadığını araştırmak için kullanılır en kısa tabiriyle diyip lafı daha fazla uzatmadan Tek Yönlü ANOVA’nın varsayımlarını da hatırlatarak bir an önce çözümlemeye geçelim.

ANOVA’nın sağlaması gereken başlıca 3 tane varsayımı vardır. Eğer bu varsayımlar sağlanmadığı takdirde ANOVA’nın Parametrik Olmayan İstatistiksel Yöntemlerdeki karşılığı olan Kruskal Wallis Testi kullanılır.

Tek Yönlü ANOVA’nın Sağlaması Gereken Varsayımlar:

1-) Grupların birbirinden bağımsız olması

2-) Normallik varsayımına uyması

3-) Varyansların homojenliği(eş varyanslılık)

Öncelikle veri setine buradan ulaşabilirsiniz. Hemen Python’dan ilk önce gerekli kütüphaneleri yükleyelim.

import pandas as pd #Veri yükleme DataFrame liste gibi yapıları kuran düzenleyen kütüphane
import scipy.stats as stats #İstatistiksel fonksiyonları barındıran kütüphane
import researchpy as rp #Pandas, stats gibi kütüphaneleribir araya getiren yardımcı kütüphanedir
from statsmodels.stats.multicomp import pairwise_tukeyhsd #Çoklu Karşılaştırma testi için gerekli kütüphanenin bir modülü 
from statsmodels.stats.multicomp import MultiComparison # Çoklu karşılaştırma testi için gerekli kütüphanenin diğer bir modülü

Eğer yukarıda ki kütüphaneler bilgisayarınızda yoksa ve Anaconda Spyder kullanmıyorsanız Windows kullanıcıları için Komut Satırı Linux kullanıcıları için ise Konsole’dan aşağıdaki şekilde yükleyebilirsiniz. Ben Manjaro Linux kullanıyorum. Spyder yüklemek için gerekli koda da aşağıdan ulaşabilirsiniz(Manjaro Linux veya Arch Linux sistemlerinden birini kullanıyorsanız).

pip install spyder #Spyder IDE kurulumu
pip install pandas #Pandas kütüphanesi kurulumu
pip install scipy #Scipy kütüphanesi kurulumu
pip install researchpy #Researchpy kütüphanesi kurulumu
pip install statsmodels #Statsmodels kütüphanesi kurulumu

Gerekli kütüphaneleri ve kütüphanelerin nasıl yükleneceği bilgilerini verdikten sonra verimizi yükleyelim ve inceleyelim. Ben veriyi analiz ederken Spyder kullandım ve Spyder’da File Explorer kısmında veri neredeyse o kısma girdim bu yüzden tam uzantıyı yazmama gerek kalmadı veriyi yüklerken. Eğer siz File Explorer kısmından verinin bulunduğu konuma gitmiyorsanız verinin dizinini belirtmeniz gerekiyor.

anova_data = "data.csv" #Veri
df_anova = pd.read_csv(anova_data) #Pandas yardımıyla veri yüklendi
df_anova.head() #Verinin ilk 5 satırı
df_anova.tail() #Verinin son 5 satırı veri setimizde 29 veri olduğu görülüyor

Pandas ile verimizi yükleyip head() fonksiyonuyla verinin ilk 5 satırını görüyoruz.

Yukarıdaki çıktıya baktığımızda verinin başarılı bir şekilde yüklendiğini görüyoruz. -Eğer dilerseniz tail() fonksiyonu yardımıyla son 5 satırı görebilirsiniz. – Ama burada Sıra değişkeninin bize pek bir yararı yok bu yüzden bu değişkeni(sütunu) çıkartsak analizde işimiz daha kolay olur gibi geliyor.

df_anova.drop("Sıra", axis = 1, inplace = True)
df_anova.head()

Evet drop() fonksiyonuyla “Sıra” değişkenini veriden çıkarttık ve daha güzel bir hale geldi verimiz. Ama tabiki de işimiz bitmedi Grup değişkeninde sayısal veriler var bunları kategorik veriye dönüştürmemiz gerekli ve bunlara grup ismi versek daha güzel hale gelir gibi duruyor. Bunun için Python Dictionary(Sözlük) yapısını kullanabiliriz.

df_anova["Grup"].replace({1:"grup1",2:"grup2",3:"grup3"}, inplace = True)

Şimdi Özetleyici İstatistiklere bakabiliriz.

rp.summary_cont(df_anova["Ağırlık"].groupby(df_anova["Grup"])) #Desc Stat

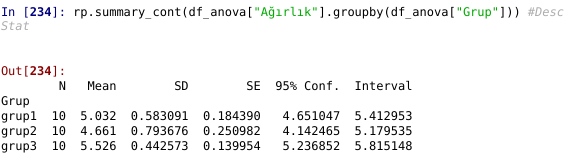
Yukarıdaki özetleyici istatistiklerden grupların ortalamalarını, standart sapmalarını, standart hatalarını güven aralıklarını görebiliriz. Grup2’in Grup1 ve Grup3’e göre ortalamasının düşük ve standart sapmasının yüksek olduğu görülüyor bu belki ileride fark yaratan grup olabilir.

Şimdi verimiz analiz için uygun olduğuna göre ve ön bilgiler edindiğimize göre varsayımlara bakıp analizimize geçebiliriz.

Varsayım 1 : Grupların birbirinden bağımsız olması

Kullandığımız veri setinin içeriğini tam olarak bilemediğimizden ötürü grupların birbirinden bağımsız olduğunu düşünüyoruz ve ilk varsayımın kabul edildiğini düşünüyoruz.

Varsayım 2 : Verilerin Normal Dağılıma Uyması

Bu varsayımı test etmeden önce hipotezimizi kurmalıyız.

Ho: Verilerin dağılımı ile Normal Dağılım arasında fark yoktur.(Veriler normal dağılıma uygundur.)

Hs: Verilerin dağılımı ile Normal Dağılım arasında fark vardır.(Veriler normal dağılıma uygun değildir.)

Hipotezlerimizi kurduğumuza göre şimdi test edebiliriz. Veri sayımız az olduğu için Shapiro Wilks testini kullanabiliriz. Eğer veri sayımız biraz daha fazla olsaydı Kolmogorov Smirnov testi kullanmamız gerekirdi. Gerçi son zamanlarda bu iki testi pek çok kimse ayrımını yapmıyor ama olsun 🙂

stats.shapiro(df_anova["Ağırlık"]) #Ho reddedilemez

Çıkan çıktıdaki 2. elemanımız bize p-değerini veriyor ve bu değer α = 0.05 değerinden büyük olduğu için yokluk hipotezimiz(Ho hipotezi) reddedilemez. Yani verilerin dağılımının normal dağılımdan farkı olmadığını %95 güvenilirlikle (%5 yanılmayla) istatistiksel olarak söyleyebiliriz. Bu varsayımımız sağlandığına göre diğer varsayımımız olan varyansların homojenliliği ya da diğer bir deyişle eş varyanslılık varsayımına bakalım. Öncelikle hipotezi kuralım ama.

Ho: Varyanslar arasında fark yoktur(Varyanslar homojendir).

Hs: Varyanslar arasında fark vardır(Varyanslar homojen değildir).

stats.levene(df_anova['Ağırlık'][df_anova['Grup'] == 'grup1'],
             df_anova['Ağırlık'][df_anova['Grup'] == 'grup2'],
             df_anova['Ağırlık'][df_anova['Grup'] == 'grup3']) # Ho reddedilemez

P değerine baktığımızda hipotezimizin reddedilmediğini(p-değeri > α = 0.05) yani %95 güvenilirlikle varyansların homojen olduğunu istatistiksel olarak söyleyebiliriz. Varsayımlarımız sağlandığına göre ANOVA yapabiliriz artık. Ama öncelikle hipotezi kurmamız gerekiyor.

Ho: Grupların ortalamaları arasında farklılık yoktur.

Hs: Grupların ortalamaları arasında farklılık vardır.

anova_sonuç = stats.f_oneway(df_anova['Ağırlık'][df_anova['Grup'] == 'grup1'],
                             df_anova['Ağırlık'][df_anova['Grup'] == 'grup2'],
                             df_anova['Ağırlık'][df_anova['Grup'] == 'grup3'])
print(anova_sonuç) #Ho ret farklılık var

P değerinin α = 0.05 değerinden küçük olduğunu dolayısıyla yokluk hipotezimizin reddedildiği %95 güvenirlilikle istatistiksel olarak söyleyebiliriz.

Gruplar arasında fark var ama hangi grup bu farklılığı yaratıyor? Bunu öğrenmek için çoklu karşılaştırma testi yapmamız gerekiyor.

#Çoklu Karşılaştırma Testi

çkt = MultiComparison(df_anova["Ağırlık"], df_anova["Grup"])    
çkt_sonuç = çkt.tukeyhsd()
print(çkt_sonuç)

Bu karşılaştırma testi sonucunda grup2 ile grup3 arasındaki ortalamaların farklı olduğu görülüyor ama farklılığa hangisinin neden olduğu belli değil. Özetleyici istatistikler tablosunda fark ettiğimiz sonuca göre grup2 olabilir gibi geliyor ama kesin değil tabiki de bu sonuç.

Bu yazımızın da sonuna gelmiş bulunmaktayız. Yazımı burada noktalıyorum. Daha çok analizlerle görüşmek dileğiyle 🙂