Kategorik Veri Analizi ve Shiny Web Uygulamaları – 2

Mustafa Nayansak 27 Aralık 2018 Uygulama 0 2478 2602 kelime - 17 dakika57

Bu yazıya puan ver

(No Ratings Yet)

Müşterileriniz tarafından terk mi ediliyorsunuz? Ölçemediğiniz fırsat maliyetlerini azaltmak istiyor ancak nereden başlayacağınızı bilemiyor musunuz? İlk yapmanız gereken, zamanında terk-i diyar etmiş müşterilerinizin verilerini bulup getirmek… Çünkü veri ölçebilmeyi, ölçebilmek ise yönetebilmeyi beraberinde getirir.

Bir müşterinin sizi terk edip etmemesi geçmişte yaptığınız reklam harcamaları ile veya izlediğiniz bazı politikalarla bir neden sonuç ilişkisine dayandırılarak modellenir. Terk etme potansiyeli olan bir müşterinin sizi terk edip etmeyeceğini tahmin etmek istiyorsanız elinizde güçlü bir model olması gerekir ve bu modeli elde etmek için ise öncesinde birçok kez terk edilmeniz 🙂

Doğru örnekleri yakalayabilen, güçlü tahminler yapabilen bir Lojistik Regresyon Modeli kurmak istiyor ve daha fazla terk edilmek istemiyorsanız gelin, neler yapabileceğimize beraber bakalım.

İkili Lojistik Regresyon

Önceki yazımda lojistik fonksiyon, lojistik regresyon modeli, logit dönüşümü işlemi hakkında bilgiler vermiştim, tekrar gözden geçirmek gerekirse;

Regresyon modeli

Kitle doğrusal regresyon modeli

Kitle lojistik regresyon modeli

– Kitleye ait doğrusal hale getirilmiş lojistik regresyon modeli. ise yaptığımız dönüşüm transformasyonunu belirtiyor.

Kitle elimizde olmadığı durumlarda örneklemlerden hareket ediyoruz, dolayısıyla kuracağımız model aşağıdaki gibi olacaktır.

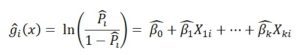
β parametresi tahmin edilirken çeşitli tahmin edicilerden yararlanılır. Örneğin, Maksimum Olabilirlik Kestiricisi tutarlılık, yeterlilik, yansızlık, etkinlik(bu kavramları matematiksel istatistik kitaplarından kolaylıkla öğrenebilirsiniz) gibi özelliklerin hepsini sağlayan, istatistiksel açıdan en çok kullanılan, yeni bir kestirici önerildiğinde de ilk karşılaştırılan kestirim yöntemidir. En Küçük Kareler yöntemi ise hata kareler toplamını en küçüklemeyi amaçlayan istatistiksel bir yöntemdir. Ancak bu yöntem sapan değerlerden fazlaca etkilenir ve daha dayanıklı bir yöntem olan En Küçük Medyan Kareler yöntemi ile kullanılması önerilir. Doğrusal Regresyon, normallik varsayımı altında çalıştığı için Maksimum Olabilirlik Yöntemi ve En Küçük Kareler Yöntemi aynı özellikleri gösterir. Eğer hataların dağılımı normal değil ise EKK, MLE’den farklı sonuçlar verir.

Lojistik Regresyon Modelinde β parametrelerini tahmin etmek için Maksimum Olabilirlik Kestiricisi kullanılır.

Şimdi teorik bilgiler denizinden çıkıyor ve en sevdiğimiz konular olan hipotez testleri, model anlamlılıkları konusuna giriş yapıyoruz.

Model Anlamlılığının Testi

En az bir sıfırdan farklıdır j=1,2,…,k şeklinde kurulan hipotez ile hariç tüm bağımsız değişkenlerin bağımlı değişken üzerindeki etkisi araştırılır.

Sapma Değeri(D):

Sapma(Deviance) Değeri, hangi modeli tahmin ediyorsanız, o modele ait olabilirlik fonksiyonudur.

Olabilirlik Oran Test İstatistiği(G) :

Lojistik regresyonda modelin anlamlılığının test edilmesi için en çok kullanılan istatistik Olabilirlik Oran test istatistiğidir.

Paydaki ifadeye 1 numaralı model dersek eğer, bu ifade 1 numaralı modelin sapma değeri olur. Bu modelde sadece bulunuyor. Paydadaki ifadeye 2 numaralı model dersek, bu ifade de 2 numaralı modelin sapma değeri olur. Bu modelde dahil tüm değişkenler modelde bulunuyor.

Lojistik regresyon modelinde model anlamlılığı için kullanılan G istatistiğinin dağılımı Chi-Square’dir. Serbestlik derecesi şu şekilde hesaplanır;

G istatistiği k serbestlik dereceli Chi-Square dağılır.

hipotezine ait karar;

veya tablodan elde edilen p değeri < ise hipotezi reddedilir. ’ın reddedilmesi, en az bir değişkeninin sıfırdan farklı olduğunu, 1- güvenle modelin anlamlı olduğunu gösterir. Hangi bağımsız değişkenin anlamlı olduğunu bulmak için teker teker katsayıları test etmemiz gerekir.

Katsayıların Anlamlılık Testi

hipotezi ile katsayıların anlamlı olup olmadığını Wald test istatistiği ile test ediyoruz.

Wald istatistiğinin örnekleme dağılımı standart normal dağılımdır.

değerleri için hesaplanan varyans kovaryans matrisinden elde edilir. Varyans kovaryans matrisi her parametre için toplamda (k+1)x(k+1) olarak oluşturulur.

hipotezine ait karar;

veya p değeri = 2P(Z>|W|) ise hipotezi reddedilir. Yani anlamlılık testi yapılan değişkenin, bağımlı değişken üzerinde anlamlı bir etkisi vardır yorumu yapılabilir.

ve Parametreleri için Güven Aralıkları

Güven aralığı, belirli bir güven düzeyinde(1-α) bir parametrenin belirli bir alt değer ve üst değer arasında gösterilmesidir. Güven aralığının formül yapısı dağılımdan dağılıma değişiklik gösterse de genel yapı her zaman korunur; tahmin edilen parametreye ait nokta kestirimi, belirli bir güven düzeyi ile bulunan tablo değeri ve örneklemin standart hatası aşağıda görüldüğü gibi formüle edilir.

için nokta tahmini;

doğrusal hale getirilmiş lojistik regresyon modeli. Lojistik regresyonda önce tahmin edilir, daha sonra değeri hesaplanır.

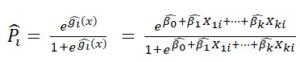şeklinde başarı olasılığı tahmin edilir.

– ‘ye ait güven aralığını oluşturmak için öncelikle ’e ait güven aralığı tahmin edilir.

şeklinde güven aralığı oluşturulur,

şeklinde kurulan model için,

şeklinde parametreleri için elde edilen varyans kovaryans tahminleri ile yukarıdaki formül uygulanır.

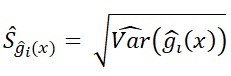standart hata ile varyans arasındaki karesel ilişkiyi kullanarak ‘in standart hatası hesaplanır. Bu işlem ile birlikte tüm değerler elde edildikten sonra için güven aralığı hesaplanır.

için alt limit değeri =

için üst limit değeri =

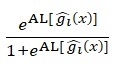
için alt limit değeri =

için üst limit değeri =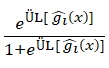şeklinde değeri için güven aralığı hesaplanır.

Yukarıdaki formüllerin elle uygulaması aşamasında birçok karmaşık matematiksel işlem bulunmaktadır. Bu aşamaları daha iyi anlamak adına önceki yazımda kullandığım kalp hastalığı ile ilgili olan veri ile model anlamlılık testleri, değişkenlerin anlamlılık testleri ve güven aralıkları hakkında R programı ile uygulama yapacağız.

Araştırmada, kişinin yaşının kalp hastası olup olmaması üzerinde anlamlı bir etkisinin olup olmadığı araştırılıyor.

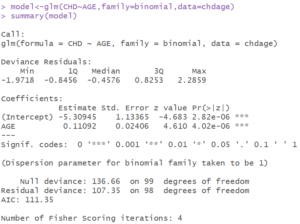
Modeli kurarken glm() fonksiyonunun içinde kullanılan parametrelerden bir tanesi olan family parametresi ile uygun olan regresyon tercih edilir. glm(Generalized Linear Models) fonksiyonu birden fazla regresyon modeli içeren bir fonksiyondur. Örneğin family = binomial ile lojistik regresyon, family=gaussian ile doğrusal regresyon, family=poisson ile loglinear regresyon kullanabilirsiniz.
Şekilde görüldüğü üzere ve parametrelerinin tahmincilerini, standart hatalarını hesaplanan Z ve değerlerini görüyoruz. Kestirim değerlerini kullanarak model kuruyoruz, standart hataları kullanarak katsayıların anlamlılıklarını test ediyoruz, değeri ile katsayının anlamlı olup olmadığına karar veriyoruz.
Full modelin sapma değeri 136.66, azaltılmış modelin sapma değeri 107.35 olarak bulunmuş ve bu iki değerin farkı bize g istatistiğini veriyor. Bu değerlerin yanlarında ise serbestlik derecelerini görüyoruz ve bu değerlerin farkı da Chi-Square değerinin serbestlik derecesi olan k değerini veriyor.
AIC olarak belirtilen Akaike Bilgi Kriteri, iki model arasında seçim yapmak için kullanılmaktadır. Burada tek bir değişkenlerle ilgilendiğimiz için bu değeri kullanmamıza gerek yok. İlerleyen çalışmalarda bu bilgiyi çoklu lojistik regresyon modelinde model tercih etme işlemlerinde kullanacağız.

Model

gözleme ait model tahmin edilir.

Model Anlamlılığı Testi

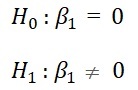
Modelde tek bir bağımsız değişken olduğu için sadece bir değişkenin anlamlılığı test edilir ve değişken anlamlılığı için kullanılan Wald test istatistiği veya model anlamlılığı için kullanılan G test istatistiği ile model anlamlılığı test edilebilir.

G test istatistiği ile model anlamlılığı testi (α=0.05)

İlk olarak azaltılmış modelin deviance’ından tam modelin deviance’ını çıkararak bir G test istatistiği elde ediyoruz.

Elde ettiğimiz test istatistiğinin dağılımı, k serbestlik dereceli Chi-Square olduğu için bir Chi-Square değeri hesaplıyoruz ve test istatistiği ile bu değeri karşılaştırıyoruz. Eğer g istatistiği tablo değerinden büyük ise model anlamlıdır diyoruz.

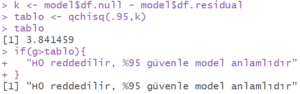
Aynı hipotezi p-değeri ile alpha değerini karşılaştırarak test edebiliriz.

Görüldüğü üzere hesaplanan p değeri 0.05 olan alpha değerinden küçük olduğu için hipotezi reddedilir.

Wald test istatistiği ile model anlamlılığı testi

Yukarıda summary() fonksiyonu ile elde ettiğimiz tablodan değişkeninin tahmin değerini ve standart hata değerini kullanarak bir Wald test istatistiği hesaplıyoruz.

Wald test istatistiğinin dağılımı standart normal dağılımdır.

Burada dikkat edilmesi gereken nokta, normal dağılımın iki yönlü simetrik bir dağılım olmasıdır. Dolayısıyla değeri ile karşılaştırılması gerekir.

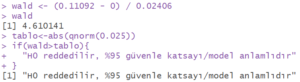
Not : Uygulamada yazılan tüm fonksiyonlar ve çıktılar görsel olarak verilmiştir. Aşağıda, uygulamada kullanılan fonksiyonlara ulaşabilirsiniz. Ek olarak aynı veri seti üzerinde farklı işlemler yapmak isteyen arkadaşlar bana mail yoluyla ulaşabilirler.

model <- glm(formula = CHD~AGE,family=binomial,data=chdage_csv)
summary(model)

g<-model$null.deviance-model$deviance
g

k <- model$df.null-model$df.residual
tablo <- qchisq(0.95,k)
tablo

if(g>tablo){
  "H0 reddedilir, %95 güvenle model anlamlıdır"
}

p.degeri <- 1-pchisq(g,k)
p.degeri

wald <- (0.11092-0) / 0.02406
wald 

tablo <- abs(qnorm(0.025))
if(wald>tablo){
  "H0 reddedilir, %95 güvenle katsayı/model anlamlıdır"
}

Shiny

Shiny uygulamaları geliştirme adımları, server ve ui dosyalar arasındaki etkileşim hakkında genel bilgileri öğrendikten sonra kullanılan fonksiyonlara giriş yapıyoruz. Uygulamada, en çok kullanılan fonksiyonlar ve işlevleri hakkında kısaca bilgiler verdikten sonra bir uygulama yapacağız. Bu yazı dizisinde kullanacağımız tüm istatistikleri bu uygulamanın üzerine inşa edeceğiz ve yazı dizisinin sonunda Kategorik Veri Analizi için aktif olarak kullanılabilen bir uygulama geliştirmiş olacağız.

Arayüz Düzeni

Kullanıcı arayüzünde sayfa düzeni için kullanılabilecek fonksiyonlar;

absolutepanel() : Sayfanın belirli bir noktasında sabit bir panel oluşturur.
boostrapPage() : Bootstrap kütüphanesi yüklenir. Bootstrap yazılım iskeleti olarak bilinir ve HTML, CSS ve JavaScript kodunun bileşimi olarak kullanılır.
conditionalPanel : Koşullu panel oluşturur.
column : Sayfada kullanıcı isteklerine göre kolon oluşturur.
fixedPage : Yüksekliği ve genişliği değişken olmayan sayfa oluşturur.
fluidPage : İçerisindeki her elementin yüksekliği ve genişliği değişken ölçüleri olduğu sayfa oluşturur.
headerPanel : Sayfasının üst kısmında yer alan bir panel oluşturur.
mainPanel : Sayfanın ortasına bir ana panel oluşturur.
sidebarLayout : Sayfasnın içerisinde sağı ve solu eşit olan bölümler oluşturur.
tabpanel : Sekmeli bir panel oluşturur.
titlePanel : Sabit bir başlığı olan panel oluşturur.

Arayüz Girdileri

Girdi etkileşimleri için kullanıcıyı yönlendiren kullanıcı ara yüzü oluşturma fonksiyonları;

checkboxInput : Girdiler için checkbox ekler.
fileInput : Bilgisayarda .csv uzantılı dosyaları ekrana çağırmaya yarar.
radioButtons : Radiobutton ekler.
sliderInput : Slider ekler.
passwordInput : Şifre girdi kontrolü oluşturur.
showTab : Bir tabpanel’i dinamik olarak gizler veya gösterir.

Arayüz Çıktıları

Çıktılar için kullanıcı ara yüzü oluşturma fonksiyonları;

htmlOutput : HTML çıktıları oluşturur.
plotOutput : Nokta veya görsel çıktıları oluşturur.
verbatimTextOutput : Yazılı çıktılar üretir.
downloadButton : Bir indirme butonu veya linki oluşturur.

Uygulamalarda en çok kullanılan Shiny fonksiyonları yukarıdaki gibidir. Kullanılan bütün fonksiyonları görmek ve kullanımlarını incelemek için https://shiny.rstudio.com/reference/shiny/1.0.5/ adresinden yararlanabilirsiniz.

Uygulamaya giriş yapmadan önce uygulamanın hangi özellikleri içermesi gerektiğini taslak olarak belirlememiz gerekiyor. İlk olarak uygulamanın başka veri setlerinde de aktif bir şekilde kullanılabilmesi, modeli oluşturma adımlarında bağımlı ve bağımsız değişkenlerin açık bir şekilde belirtilebilmesi ve ekrana yansıtılacak görsellerin düzenli ve anlaşılabilir olması gerekiyor. Bu bölümde bilgisayarda bulunan .csv uzantılı bir dosyayı ekrana yansıtma işlemi hakkında bilgi vereceğim.

– ui parametresi için kullanılan fonksiyonlar

library(shiny)

ui <- fluidPage(

  # titlePanel() fonksiyonu ile uygulamaya verdiğimiz ana başlığı belirtiyoruz 
  titlePanel("Kategorik Veri Analizi"),

  # mainPanel() fonksiyonu ile bir ana panel açıyoruz ve içerisinde kullanmak istediğimiz özellikleri ekliyoruz
  mainPanel(

  # tabsetPanel() fonksiyonu ile sekmeli bir panel oluşturuyor            
  tabsetPanel(

    # tabPanel() fonksiyonu ile ilk sekmeyi açıyoruz ve bu sekmede veri okuma ve ekrana yansıtma işlemleri yapıyoruz
    tabPanel(Position="left", "Veri Okuma Islemi",
                 
                 # siderbarPanel() ile veri girdisi için bir tarayıcı, checkbox ve radioButton bulunan bir bölüm oluşturuyoruz
                 sidebarPanel(
                   
                 # br() fonksiyonu ile bir satır boşluk bırakıyoruz
                   br(),
                   
                 fileInput("file1", "Choose CSV File",
                           multiple = FALSE),
             
             checkboxInput("header", "Header", TRUE),
             
             br(),
             
             radioButtons("sep", "Separator",
                          choices = c(Comma = ",",
                                      Semicolon = ";",
                                      Tab = "\t"),
                          selected = ","),
             
             br(),
             
             radioButtons("disp", "Display",
                          choices = c(Head = "head",
                                      All = "all"),
                          selected = "head")             
        )   
    ),

    # tabPanel() fonksiyonu ile "Basit Lojistik Regresyon" adında ikinci bir sekme ekliyoruz
    tabPanel("Basit Lojistik Regresyon")  
),

              # Yukarıdaki parantez ile tabsetPanel() fonksiyonundan çıkış yapıyoruz ve uygulamanın her sekmesinde eklediğimiz
              # veri tablosunun görünür olmasını sağlıyoruz. tableOutput() ile eklenen veri tablosunu ekrana yansıtıyoruz
              tableOutput("contents")
))

Yukarıda gördüğünüz tüm fonksiyonların kullanımını aşağıdaki ekran görüntüsünde verilen kullanıcı arayüzü ile karşılaştırabilirsiniz. Bundan sonraki geliştirmelerimizi bu arayüz üzerinde yapacağız.

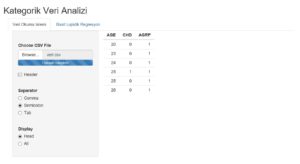
– server parametresi için kullanılan fonksiyonlar

server <- function(input, output) {

  # renderTable() fonksiyonu ile veriyi okuyup bir çıktı değişkenine aktarma işlemi yapıyoruz.
  output$contents <- renderTable({

    # req() fonksiyonu ile önce girdi değerlerinin olup olmadığı kontrol edilir, eğer bir yanlışlık varsa işlem durdurulur
    req(input$file1)

    # tryCatch() fonksiyonu ile belirli koşullar belirterek olağandışı durumların yönetimi ile ilgili işlemler yapılır
    # Örneğin aşağıda ayrıştırma ile ilgili ve verinin gösterimi ile ilgili bir problem olduğu durumlarda
    # hangi işlemleri yapması gerektiğini belirtiyoruz.
    tryCatch(
      {
        
        df <- read.csv(input$file1$datapath,
                       header = input$header,
                       sep = input$sep,
                       quote = input$quote)
        
        error = function(e) {

          stop(safeError(e))
        }
        
        if(input$disp == "head") {
          return(head(df))
        }
        else {
          return(df)
        }
        
      })
  })
  
}

# ui ve server parametrelerini tek bir dosya içerisinde açtığımız için aşağıdaki fonksiyonla birlikte uygulamayı çalıştırıyoruz
shinyApp(ui, server)

Sonuç olarak, model oluşturma adımları, modelin ve katsayıların anlamlı olup olmadığının test edilmesi, araştırılan parametrelerin güven aralıkları hakkında teorik bilgilerle beraber R programı ile bir uygulama yaptık ve Shiny’de Kategorik Veri Analizi uygulamasının ilk adımlarını atmış olduk.

İlginiz için teşekkürler.